-
旅人算(離れる②) 解答
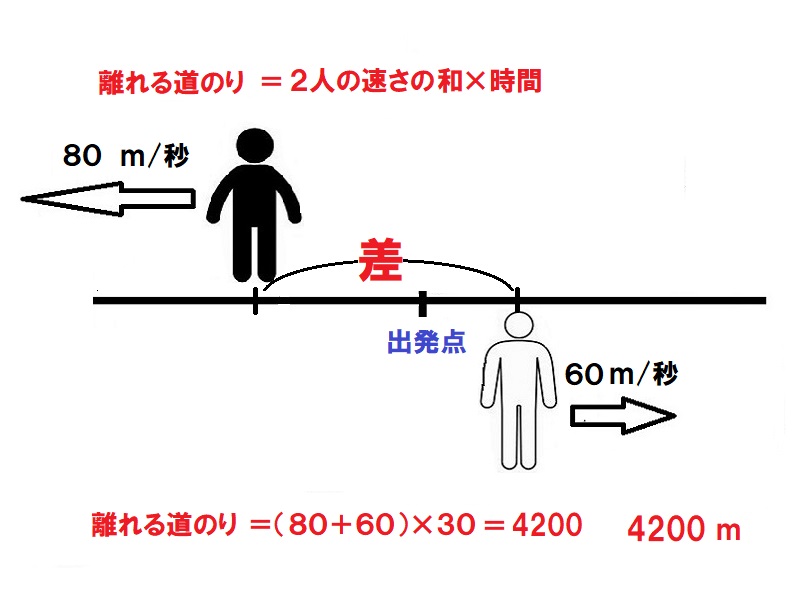
AとBとの速さの和80+60=140m/秒だけ離れる。よって、140m/秒×30秒=4200m離れる。
4200m -
旅人算(離れる①) 解答
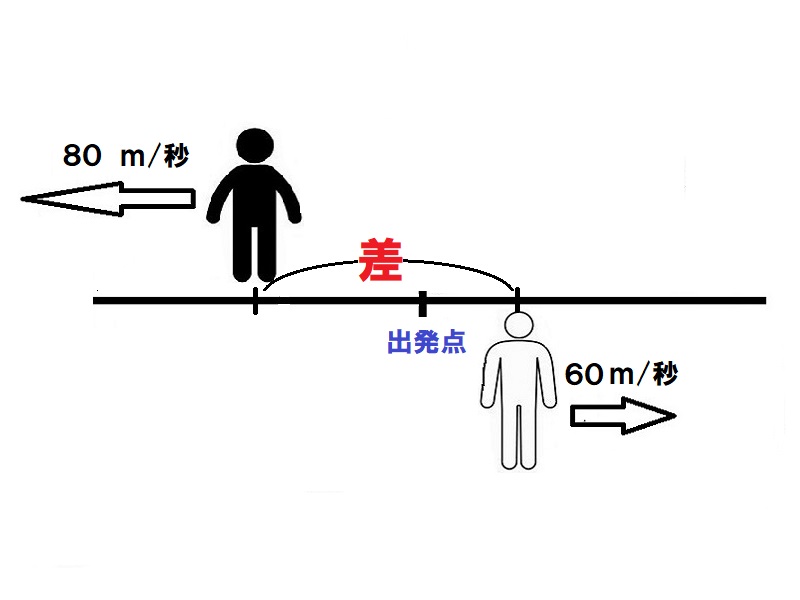
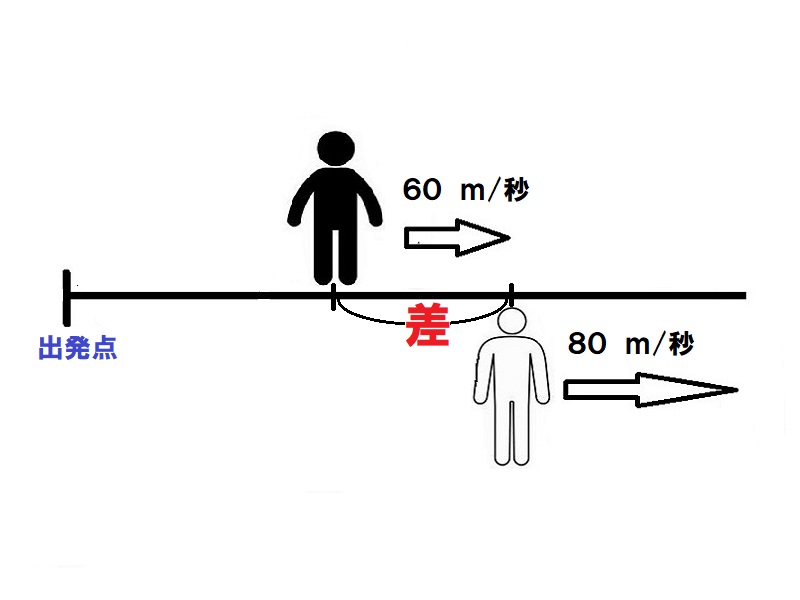
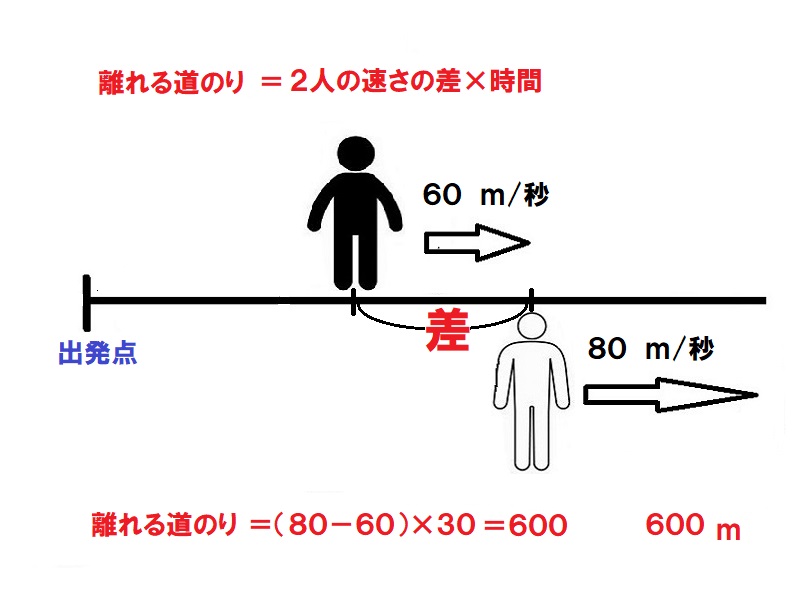
AとBの差80-60=20m/秒だけ離れる。よって、20m/秒×30秒=600m
600m -
旅人算(出会う) 解答
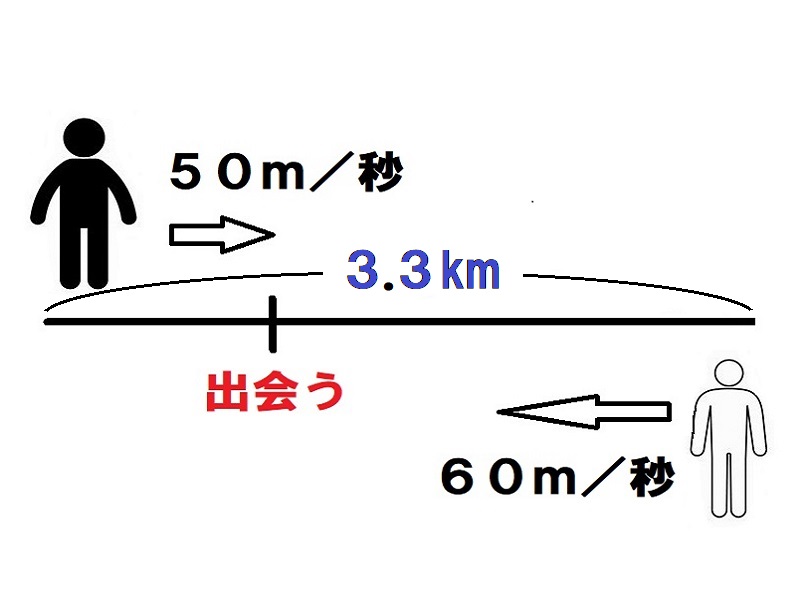
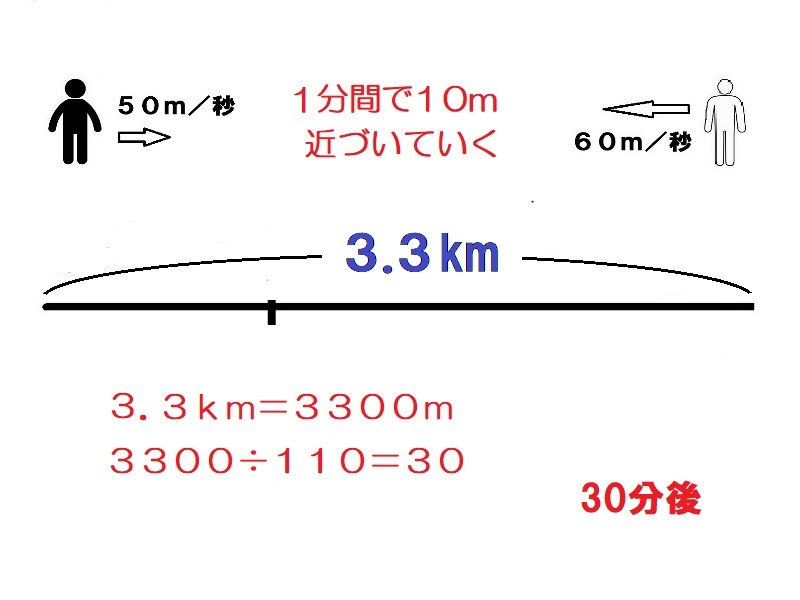
AとBは1分間に10mずつ近づいていく。よって3.3km離れているの出会うまでの時間は3300÷10=330秒(5分30秒)かかる。
5分30秒 -
旅人算(追い抜く) 解答
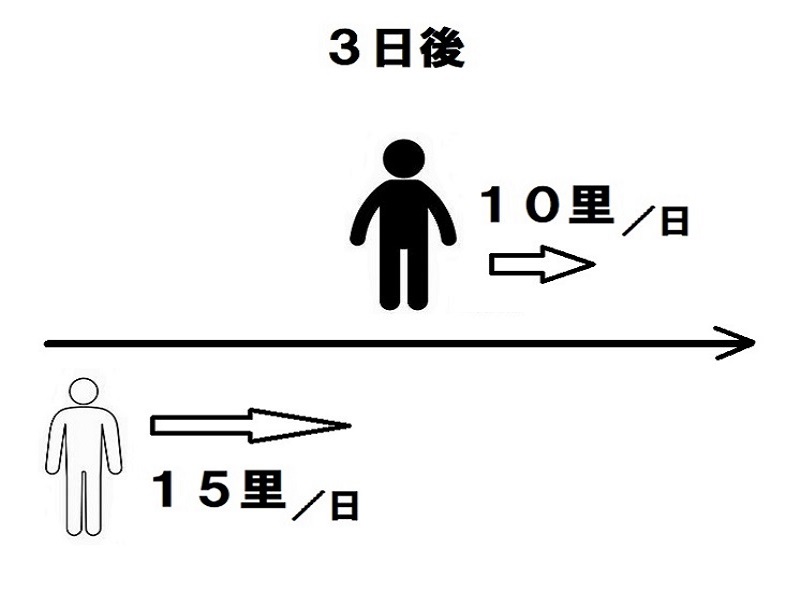
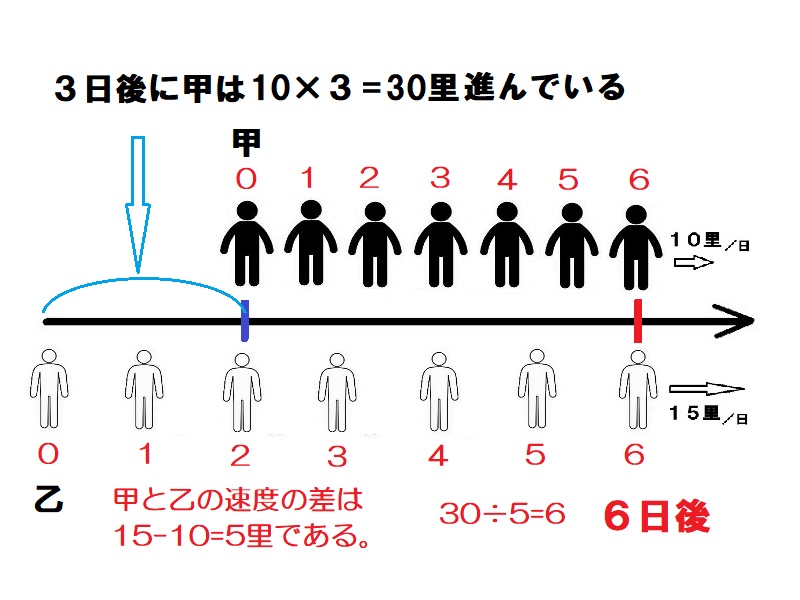
乙が出発するときには甲は10里×3=30里先に進んでいる。甲と乙の歩く速さから2人の距離は1日に15里/日ー10里/日=5里/日近づいていく。よって、追い抜くには30÷5=6日かかる。
6日 -
流水算(上る) 解答
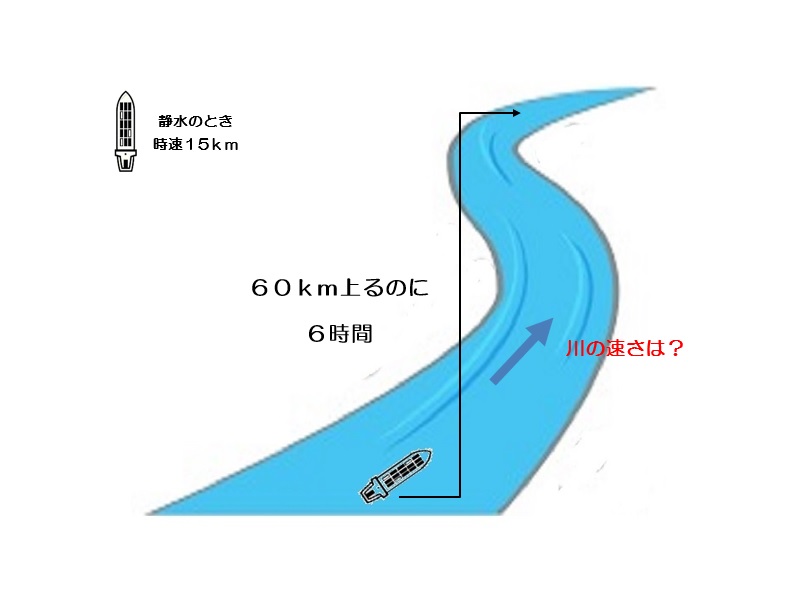
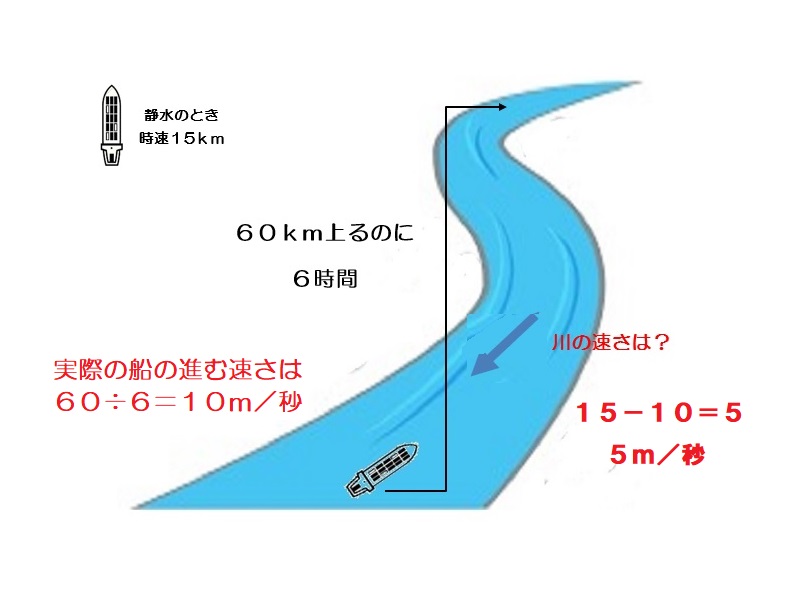
60km上るのに6時間かかるので実際の船の速さは60÷6=10km/時である。川の流れの速さは静水時の速さ-実際の川の流れの速さであるから、15-10=5である。
5km/時 -
流水算(下る) 解答
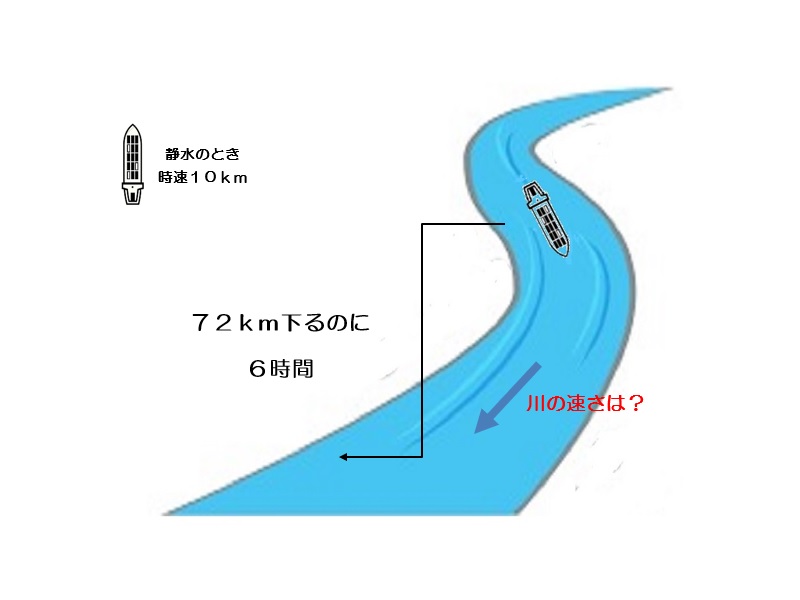
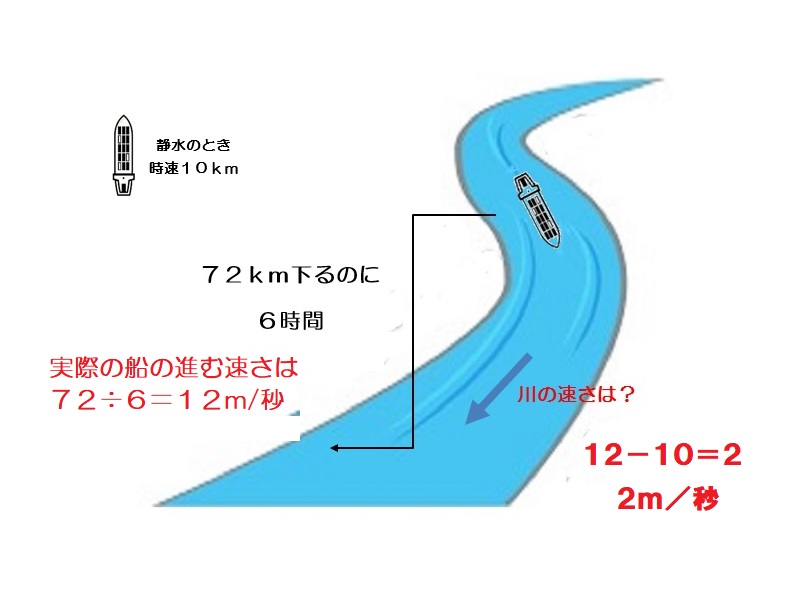
72km下るのに6時間かかるので実際の船の速さは72÷6=12km/時である。川の流れの速さは実際の川の流れの速さ-静水時の速さであるから、12-10=2ある。
2km/時 -
流水算(出会う) 解答
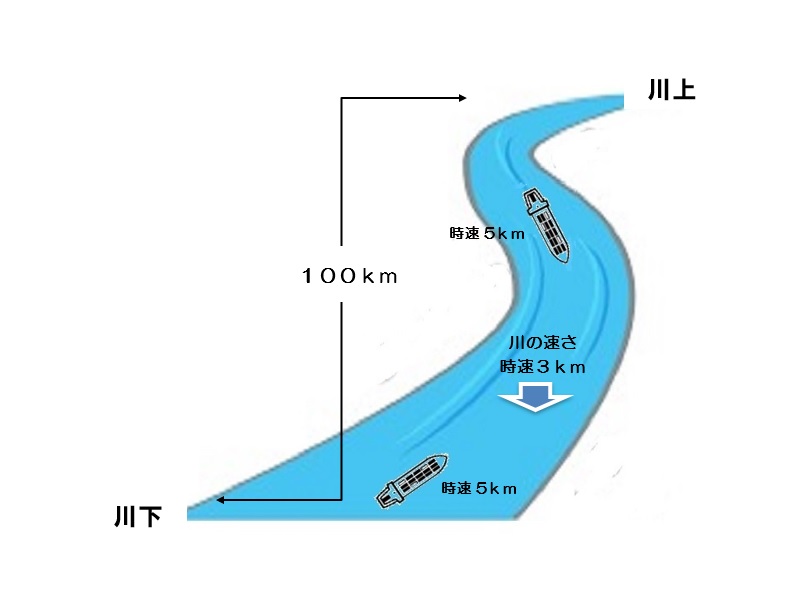
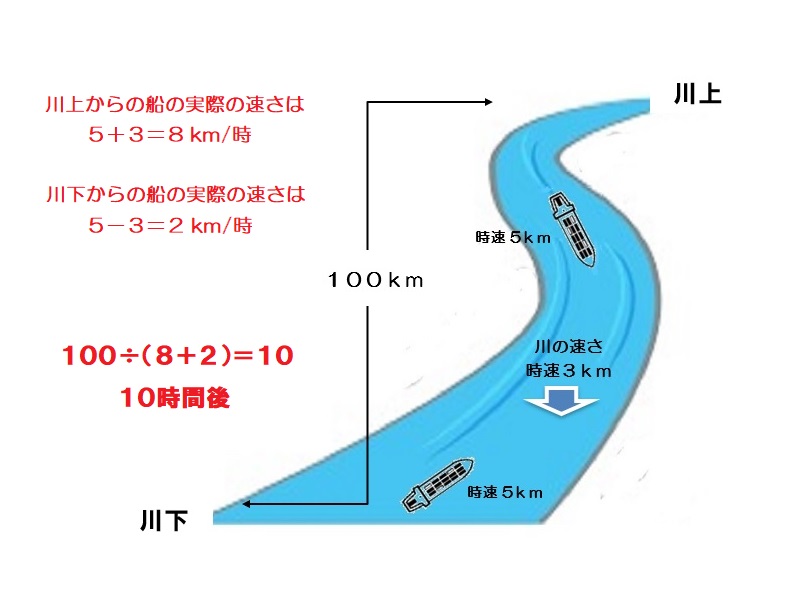
川の流れによって、上りの船の速さは5-3=2m/秒、下りの船の速さは5+3=8m/秒になる。よって2艘の船が出会うのは100÷(8+2)=10時間後になる。
10時間後 -
通過算(鉄橋を渡る) 解答
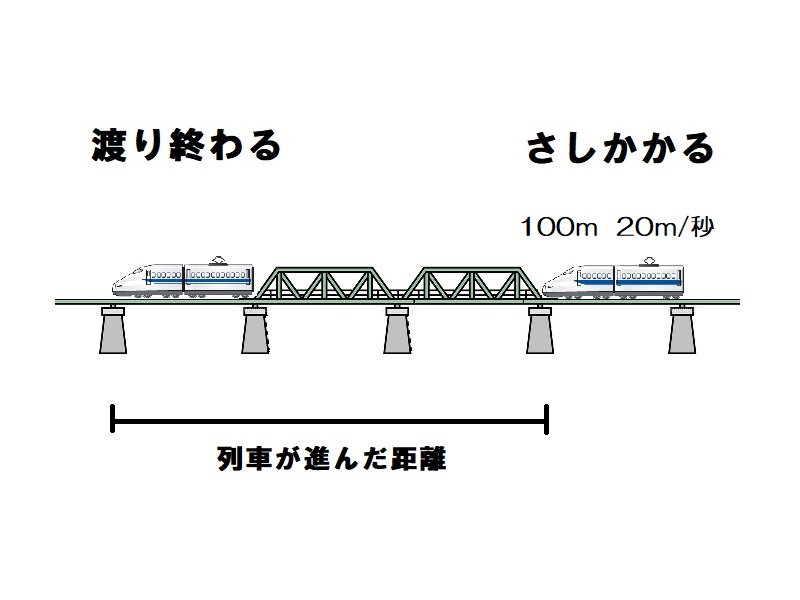
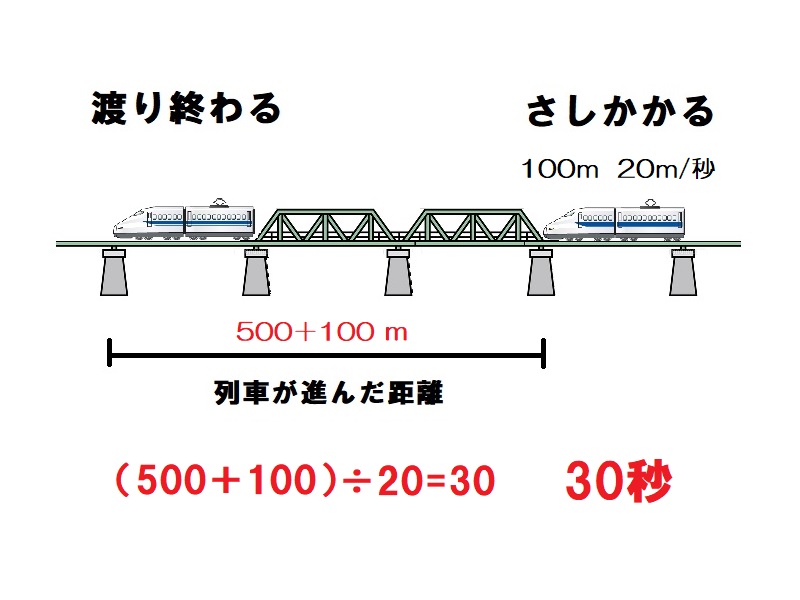
電車の先頭部分で考えると、電車が鉄橋にさしかかってから渡り終わるまでには鉄橋の長さ+電車の長さを進む。したがって、500+100=600mの距離を秒速20mで進むのでかかる時間は、600÷20=30秒である。
30秒 -
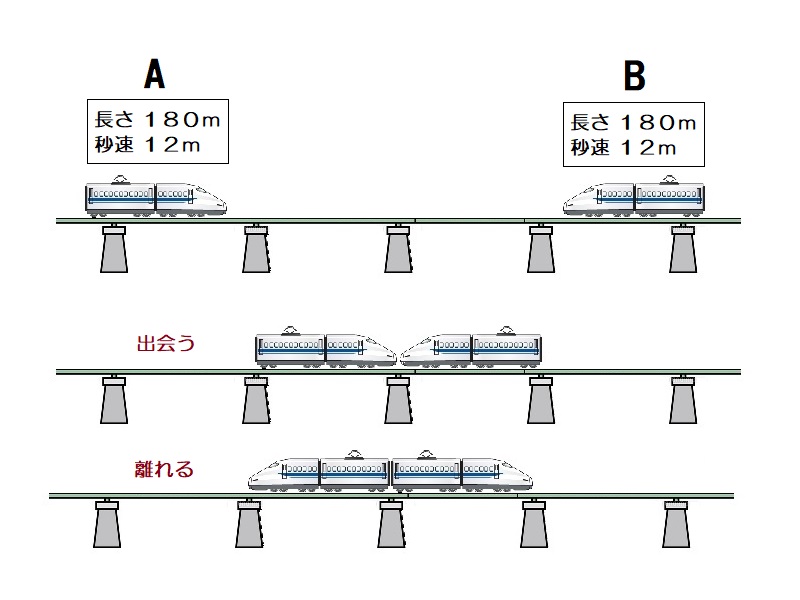
通過算(出会う) 解答
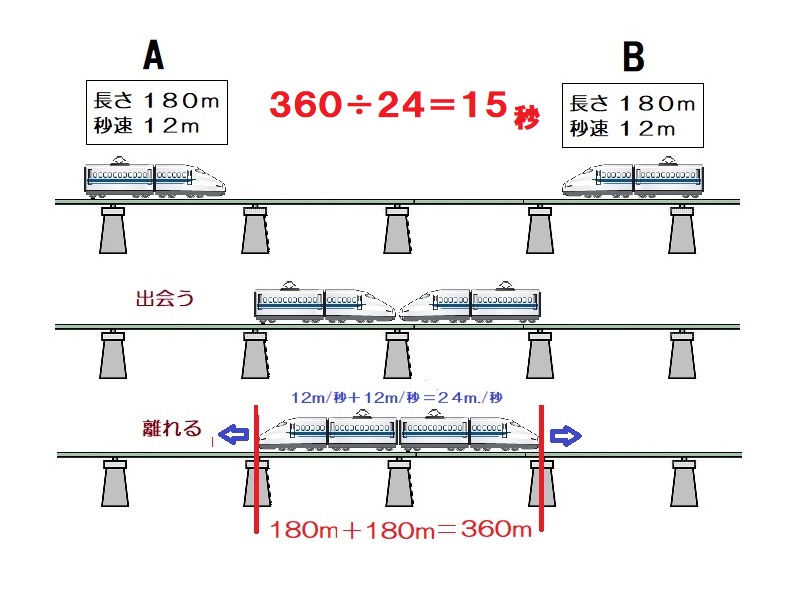
出会ってから離れるまでに進む距離は18+180=360mで、速さは12+12=24m/秒である。よって、かかる時間は360÷24=15
15秒 -
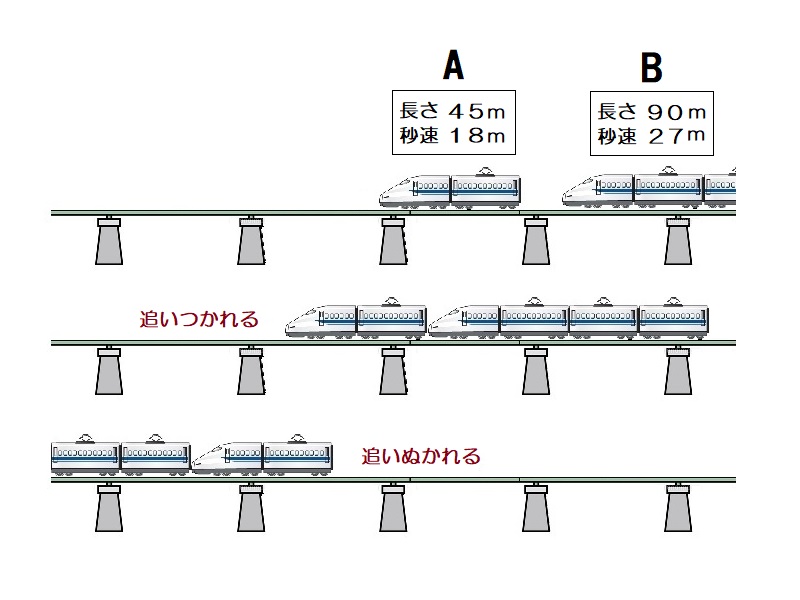
通過算(追いぬく) 解答
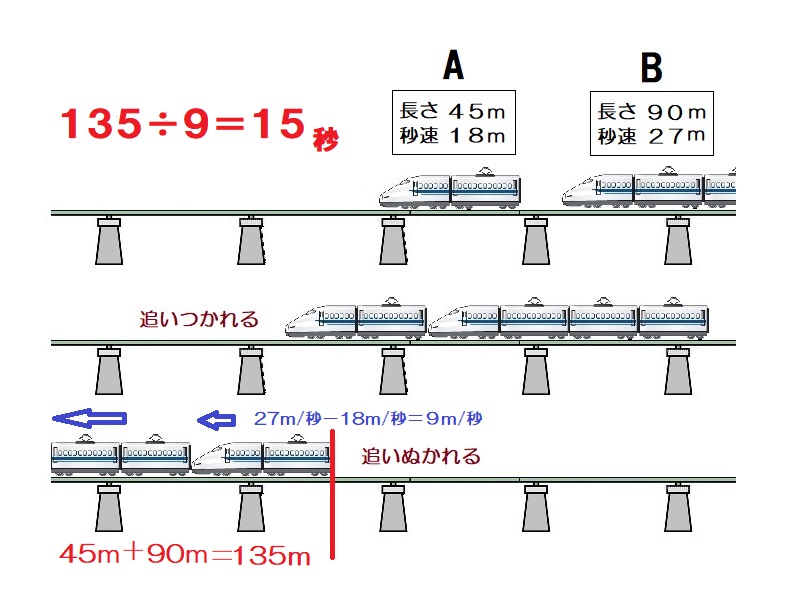
追いついてから追い越されるまでに進む距離は45+90=135mで、速さは27-18=9m/秒である。よって、かかる時間は135÷9=15
15秒 -
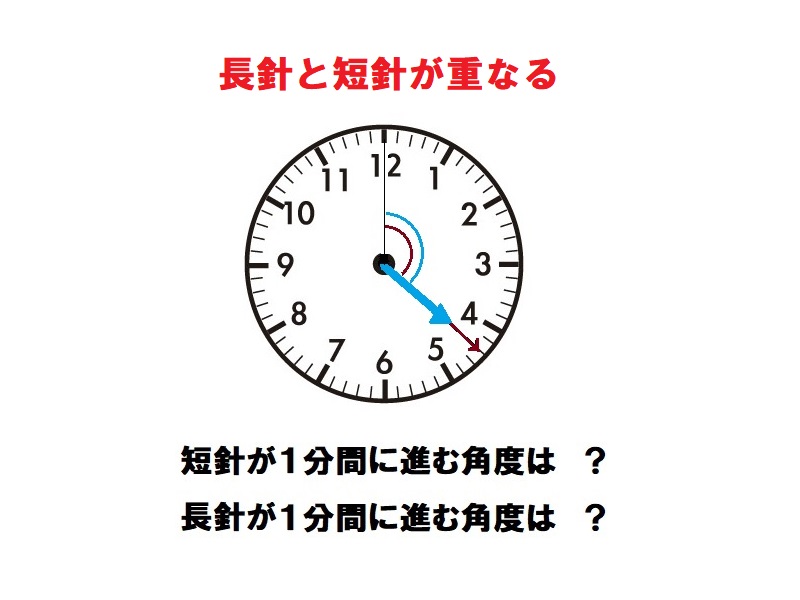
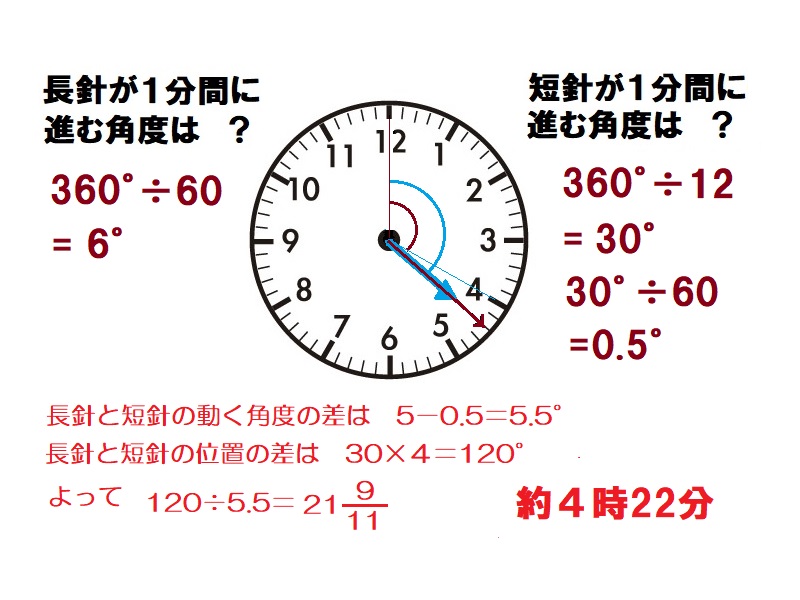
時計算(重なる) 解答
長針が1分間に進む角度は360°÷60=6°、短針が1分間に進む角度は360°÷12÷60=0.5°で短針はすでに4の所すなわち120°の所にきている。この角度を長針が1分間に6°-0.5°=5.5°で埋めていく。よって120°÷5.5°=約22分で重なる。
約4時22分 -
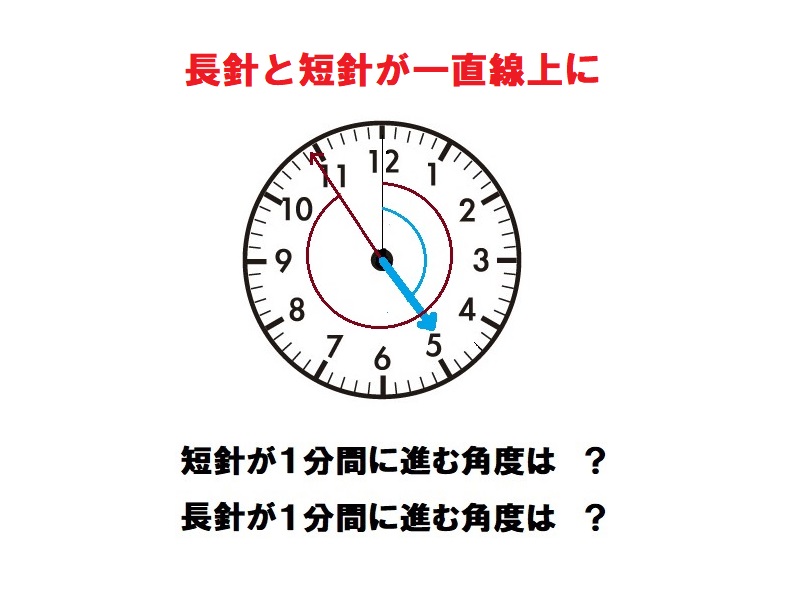
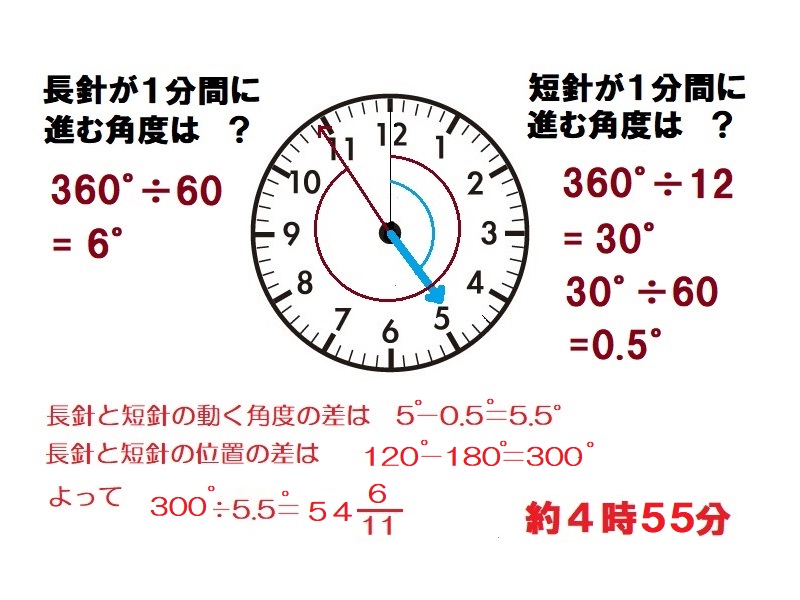
時計算(一直線) 解答
長針が1分間に進む角度は360°÷60=6°、短針が1分間に進む角度は360°÷12÷60=0.5°で短針と長針の動きの差は120°+180°=300°である。この角度を長針が1分間に6°-0.5°=5.5°で埋めていく。よって300°÷5.5°=約55分で重なる。
約4時55分 -
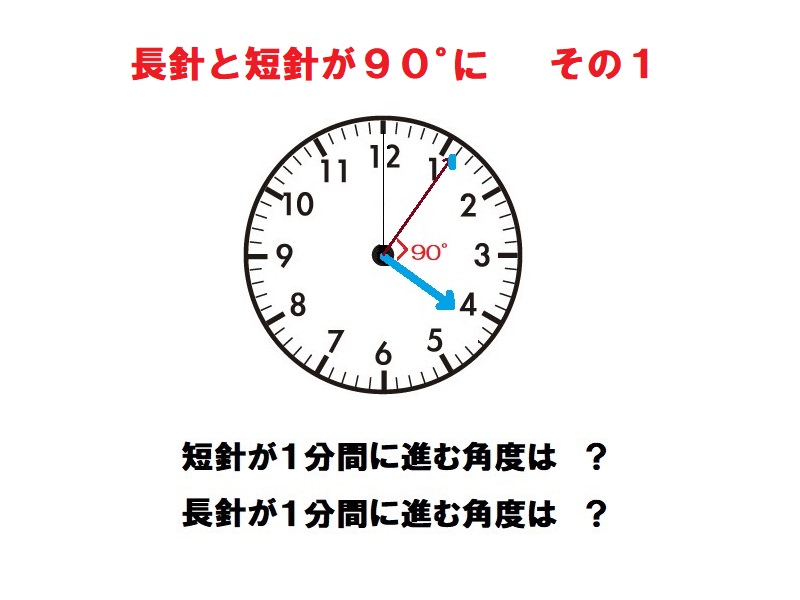
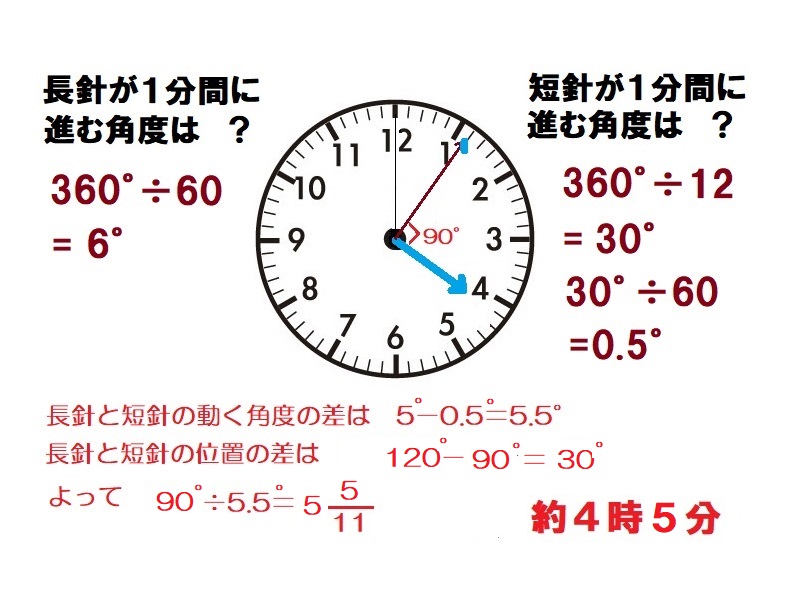
時計算(直角その1) 解答
長針が1分間に進む角度は360°÷60=6°、短針が1分間に進む角度は360°÷12÷60=0.5°である。直角と言うことは、長針と短針の角度の差が90°になるときであり、長針が120°-90°=30°の時である。この角度を長針が1分間に6°-0.5°=5.5°で埋めていく。よって30°÷5.5°=約5分で重なる。 約4時5分
-
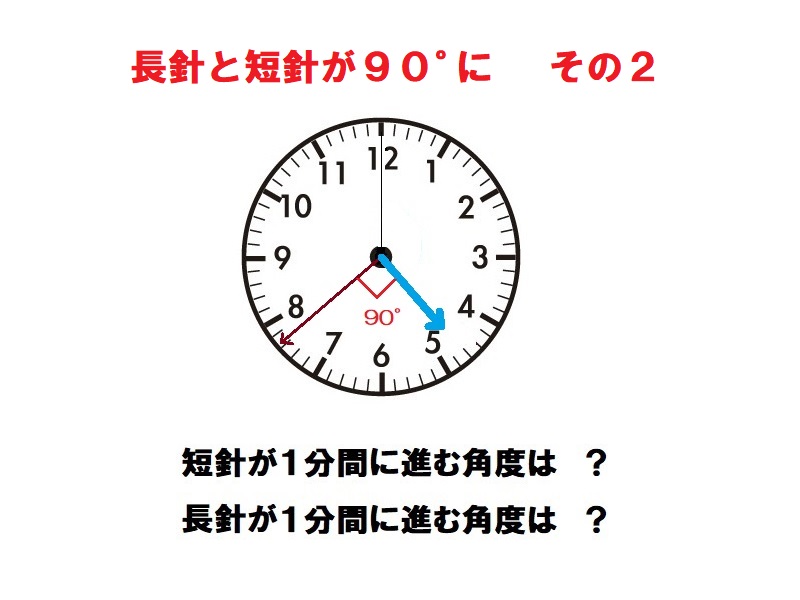
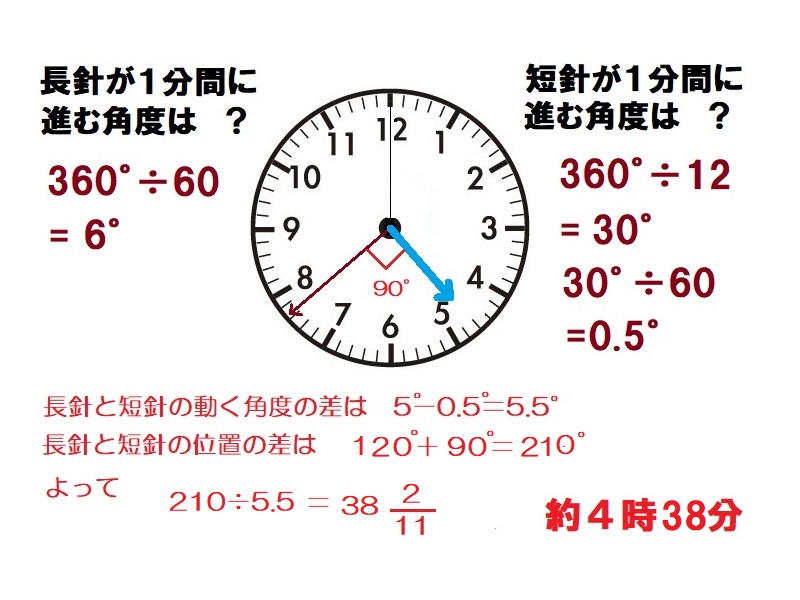
時計算(直角その2)
長針が1分間に進む角度は360°÷60=6°、短針が1分間に進む角度は360°÷12÷60=0.5°である。直角と言うことは、長針と短針の角度の差が90°になるときであり、長針が120°+90°=210°の時である。この角度を長針が1分間に6°-0.5°=5.5°で埋めていく。よって210°÷5.5°=約38分で重なる。 約4時38分
-
旅人算(反対方向で離れる)
弟は分速60m/秒、兄は分速80m/秒で、同時に同じ所から反対方向に進みました。出発してから30分後には2人の距離は何mになりましたか。
-
旅人算(同じ方向で離れる)
Aは分速60m/秒、Bは分速80m/秒で、同時に同じ所から同じ方向に進みました。出発してから30分後には2人は何m離れましたか。
-
旅人算(出会う)
3.3km離れた場所からAとBが向かい合って同時に歩き出しました。Aは分速50m、Bは分速60mです。何分後に出会いますか。
-
旅人算(追いぬく)
甲は毎日10里歩き、乙は毎日15里歩きます。甲が出発して3日後に乙が追いかけました。甲に追いつくのはそれから何日後のことでしょうか?
-
流水算(上る)
静水のときの時速が15kmの船が川を60km上るのに6時間かかります。このときの川の速さを求めなさい。
-
流水算(下る)
静水のときの速さが時速10kmの船が、川を72km下るのに6時間かかります。このときの川の速さを求めなさい。
-
流水算(出会う)
川上と川下から2隻が同時に出発します。船の速さはともに時速5kmで川上と川下の間の距離は00kmです。川が時速3kmで流れているとすると2隻が出会うのは何時間後でしょうか。
-
通過算(鉄橋を渡る)
長さ100mの列車が秒速20mの速さで走ります。この列車が長さ500mの鉄橋にさしかかってからわたり終わるまでに何秒かかりますか。
-
通過算(出会う)
AB2つの電車の長さはともに180mで、その速さもともに180m/秒です。この2つの電車が反対方向から走ってきて出会ってから離れるまで何秒かかりますか。
-
通過算(追いぬく)
速さが18m/秒で長さが45mの電車Aに、あとから速さが27m/秒で長さが90mの電車Bが近づいてきました。追いつかれてから追いこされるまでに何秒かかりますか。
-
時計算(重なる)
午後4時から午後5時までの間に、長針と短針が重なる時刻は何時何分でしょうか。
-
時計算(一直線)
午後4時から午後5時までの間に、長針と短針が一直線になる時刻は何時何分でしょうか。
-
時計算(直角その1)
午後4時から午後5時までの間に、長針と短針が90°になる時刻は何時何分でしょうか。
-
時計算(直角その2)
午後4時から午後5時までの間に、長針と短針が90°になる時刻は何時何分でしょうか。