-
決めた回数
決めた回数繰り返す
For カウンター変数=開始値 to 最終値
処理
Next カウンター変数 -
ある条件が起こるまで
ある条件が起こるまで繰り返す
Do While 条件式
処理
Loop -
二重
二重繰り返し
For カウンター変数1 = 開始値 to 最終値
For カウンター変数2 = 開始値 to 最終値
処理
Next カウンター変数2
Next カウンター変数1
-
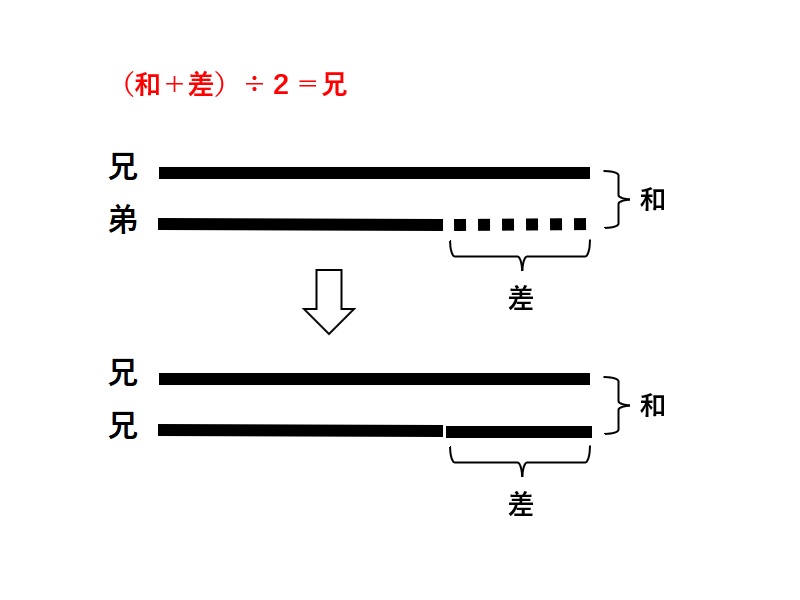
和差算 解き方1
線分図から分かるように和と差をたすと兄の2倍になる。よって4300円+500円=4800円、4800円÷2=2400円が兄の出したお金で、弟は2400円ー500円=1900円ということになる。
兄:2400円
弟:1900円 -
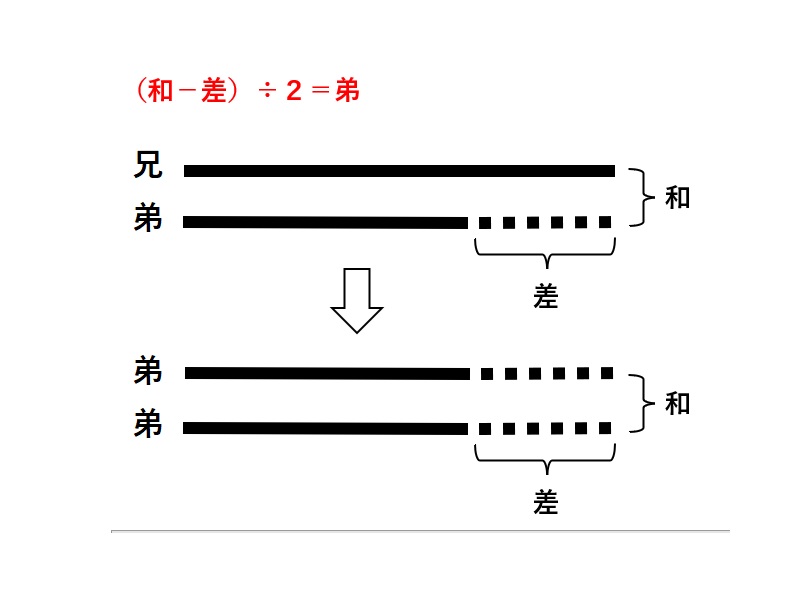
和差算 解き方2
線分図から分かるように和から差を引くと弟の2倍になる。よって4300円-500円=3800円、3800円÷2=1900円が弟の出したお金で、兄は1900円+500円=2400円ということになる。
兄:2400円
弟:1900円 -
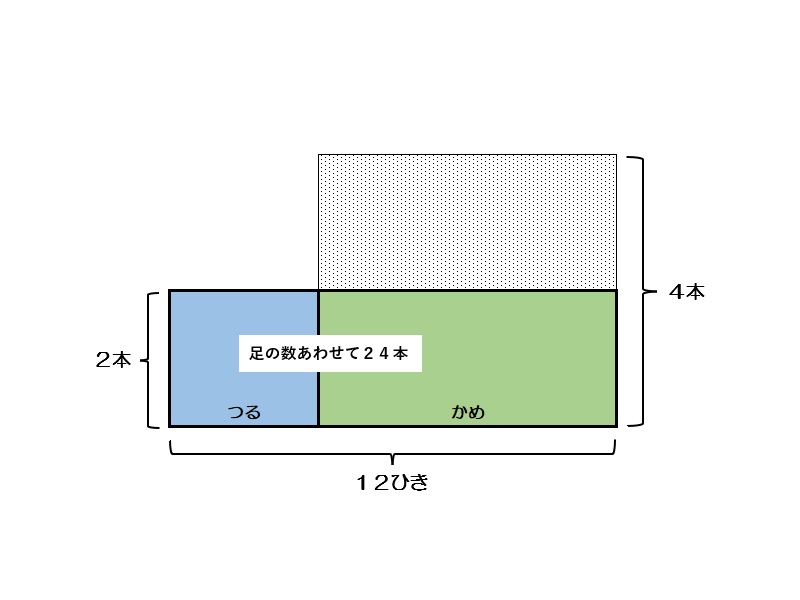
鶴亀算 解き方1
かめを仮につるとみなすとその足の数の和は2×12=24本になり、全体で40-24=16本の違いが出てくる。これは4本あるかめを2本のつると見なしたことによって出てくる差であるので、つるの数は16÷2=8羽となり、かめは12-8=4羽となる。
つる:12羽
かめ:8匹 -
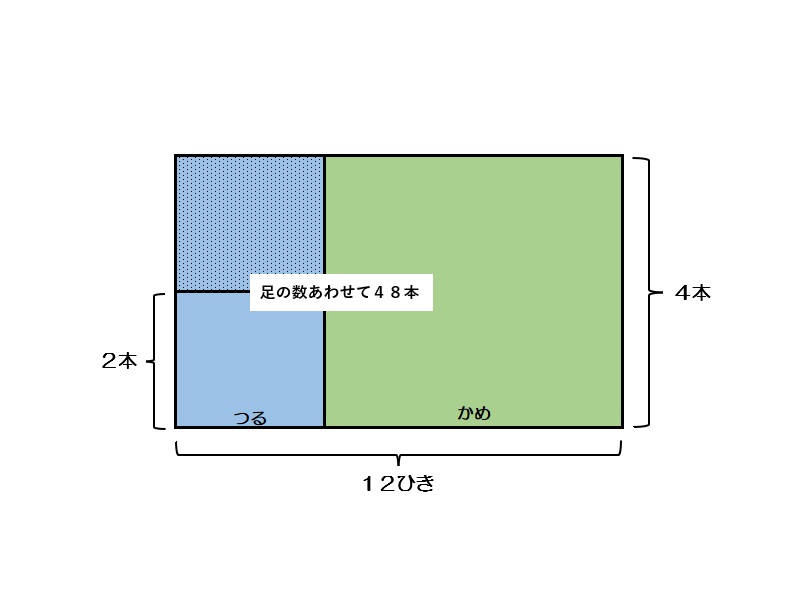
鶴亀算 解き方2
つるを仮にかめとみなすとその足の数の和は4×12=48本になり、全体で48-40=8本の違いが出てくる。これは足の数が2本のつるを4本あるかめと見なしたことによって出てくる差であるので、つるの数は8÷2=4羽となり、かめは12-4=8羽となる。
つる:12羽
かめ:8匹 -
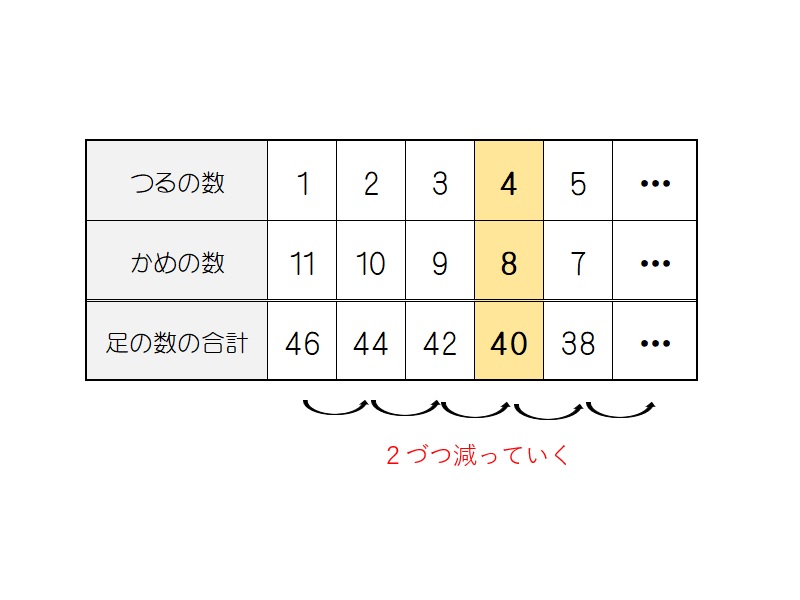
鶴亀算 解き方3
表を作って見つけることができる。つるを1から1羽ずつ増やしていくとかめは1匹ずつ減っていく。それぞれで足の数の和を計算していくと表のようになり、つるが8羽かめが4匹のとき足の数の合計が40本になる。
つる:12羽
かめ:8匹 -
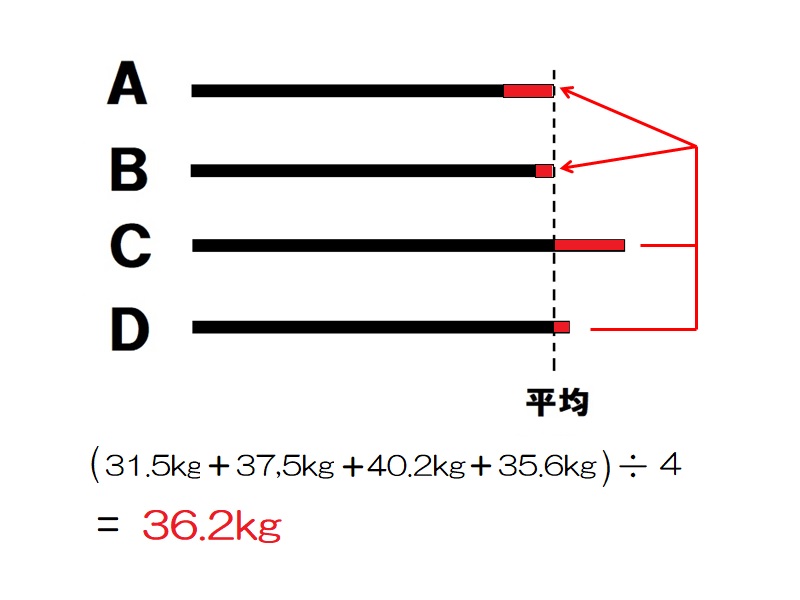
平均算 解き方1
同じ種類の数量をならして、すべて同じ大きさの数量とみることを平均するという。平均算には、平均から数量の和を求めたり、一部の平均と一部の数量から全体の数量を求めたり、平均と平均から個数を求めたり、平均と一部の数量から残る数量の大きさを求めたり、いろいろな場合がある。
36.2kg -
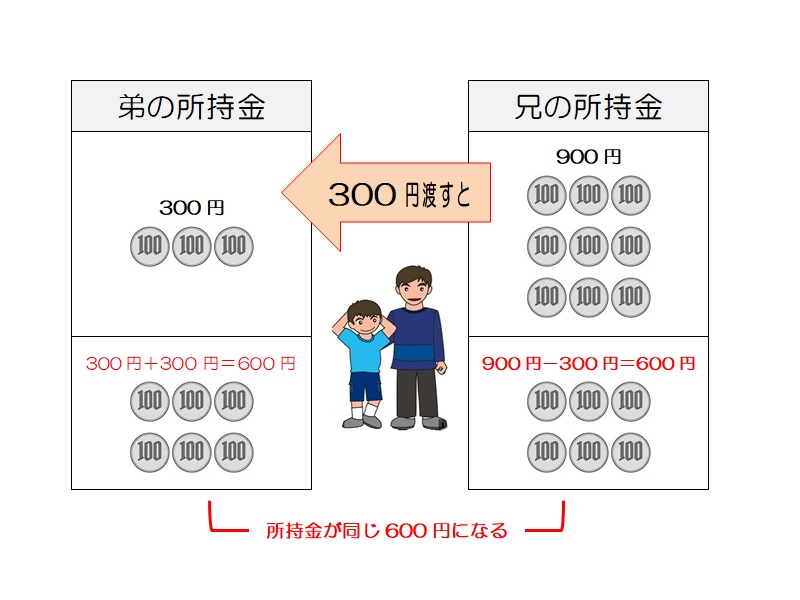
差分算 解き方1
兄が弟の所持金と同じ300円にするために600円いったん横に置いておく。そして、その600円を半分ずつ(300円ずつ)分けると、2人は同じ所持金になる。900-300=600 600÷2=300
300円 -
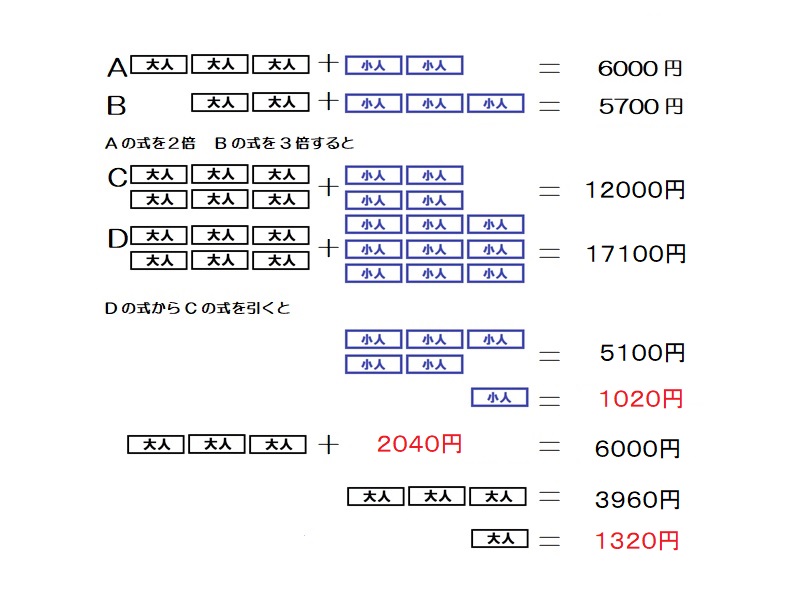
消去算 解き方1
2つの場合について、大人の人数と子どもの人数がそれぞれ違うのでどちらかを同じ人数にする。つまり、2つの場合について大人の人数を3人と2人の公倍数の6人にすることによって小人だけの値段が分かり、小人1人の入場券の値段が分かる。
大人:1320円
小人:1020円 -
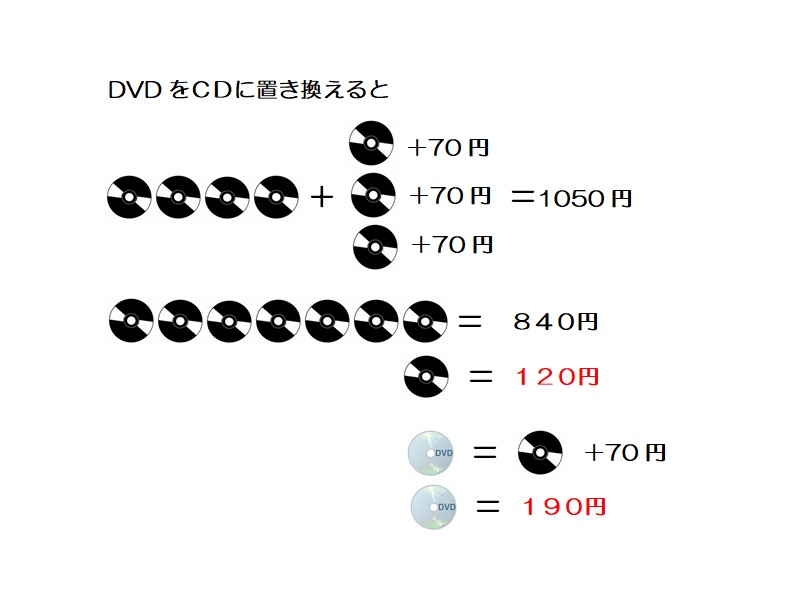
代入算 解き方1
DVD1枚をCD1枚+70円に置き換える。するとCD8枚+210円が1050円になり、そこからCD8枚が840円、CD1枚が105円であることが分かる。よって、DVD1枚は105円+70円=175円になる。
175円 -
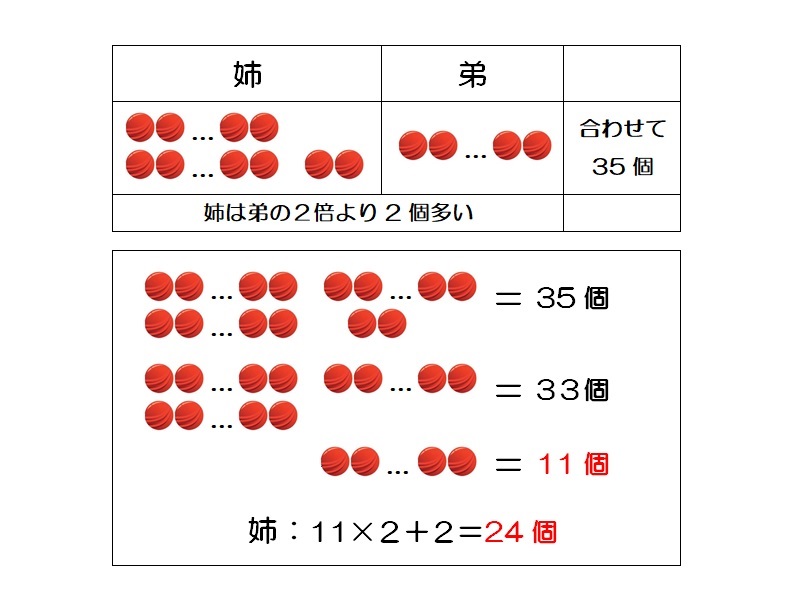
分配算 解き方1
姉は弟の2倍より2個多くなったということから、35個-2個=11個は弟の3倍の個数であることが分かる。このことから、弟は33個÷3=11個、姉は11個×2+2個=24個となる。
弟:11個
姉:24個