タイル因数分解

　タイル因数分解は、タイルを使って因数分解の答えが見つけられるだけでなく、ばらばらのものを長方形にするところに視覚的整理法が見えてきます。

タイル因数分解とは

Ｘ２とＸと１を３つのタイルで表現すると、次のように表現できます。
　　Ｘ２は１辺がＸの大きな正方形　　　
　　Ｘは縦Ｘ横１（縦１横Ｘ）の長方形　　　　　
　　１は１辺１の小さな正方形　　　　　　　　　　　
※　小さな正方形をＸ個集めると長方形になり、長方形をＸ個集めると大きな正方形になる。

下図のように、タイル操作することによって長方形に変形することがでます。このときの長方形の面積は、（Ｘ＋１）（Ｘ＋１）で表されます。つまり、Ｘ２＋２Ｘ＋１ →（Ｘ＋１）２　と変形（因数分解）できたことになります。このタイルを使って因数分解するということは、「３種類のばらばらなタイルを合わせて長方形になるように操作することであり、その因数は縦と横に現れてくる」と言えます。

いくつかの問題を解く

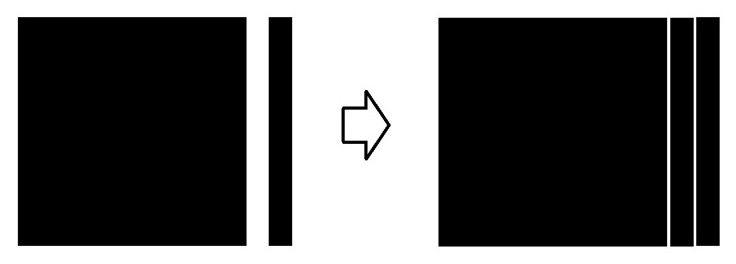Ｘ２＋２Ｘ　　　　　→ 　　　　　　Ｘ（Ｘ＋２）

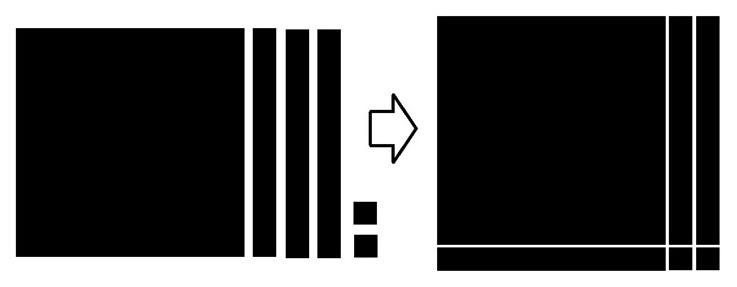Ｘ２＋３Ｘ＋２　→ 　（Ｘ＋１）（Ｘ＋２）

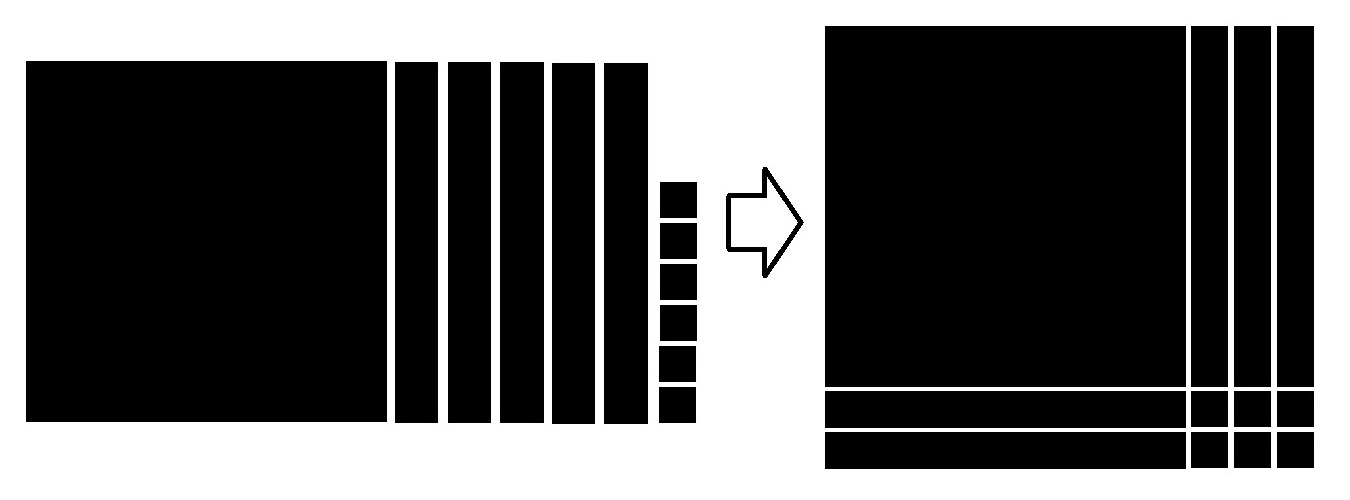Ｘ２＋５Ｘ＋６　→ 　（Ｘ＋２）（Ｘ＋３）

このような問題になると、長方形にする方法がいくつか出てくるのでおもしろい。すべての場合を見つけて、すべて正しいことを確認し合いましょう。

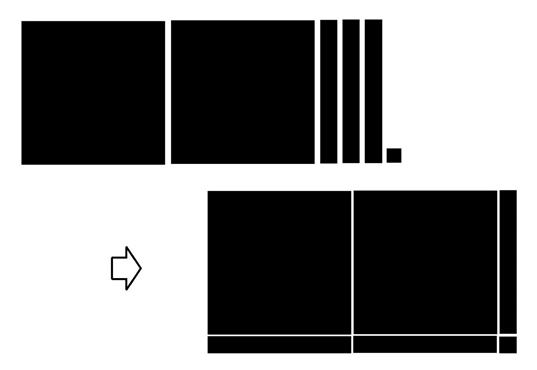２Ｘ２＋３Ｘ＋１　→ 　（２Ｘ＋１）（Ｘ＋１）

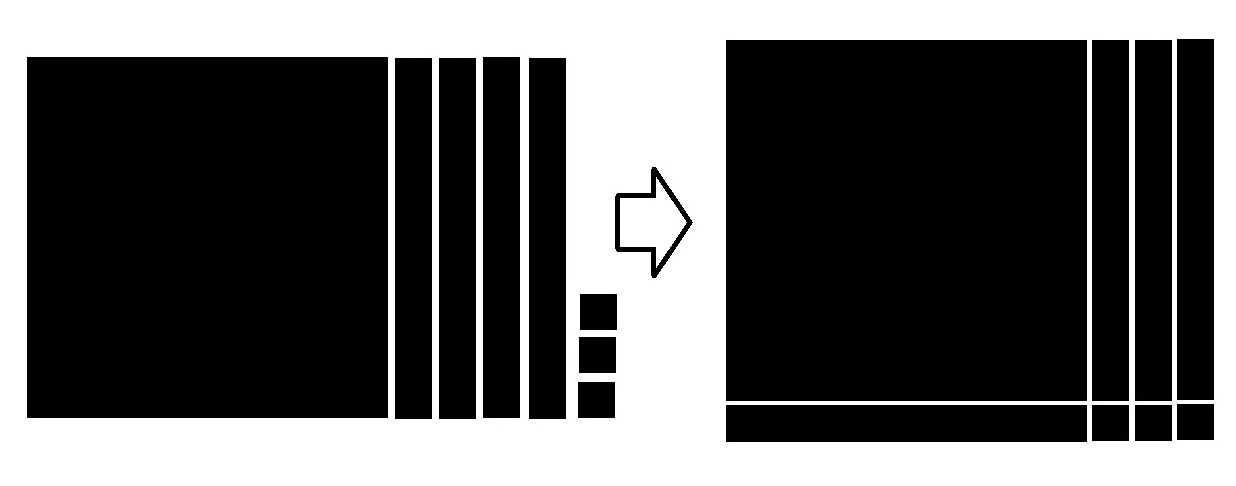
実際にタイルを作って操作をするとき、小さい正方形と大きい正方形の１辺の割合によっておかしい場合が出てきます。たとえば、大きい正方形の１辺が小さい正方形の１辺の３倍のタイルを作って、Ｘ２＋６Ｘ＋８の問題を操作させると、次のような場合が出てくるので注意が必要です。

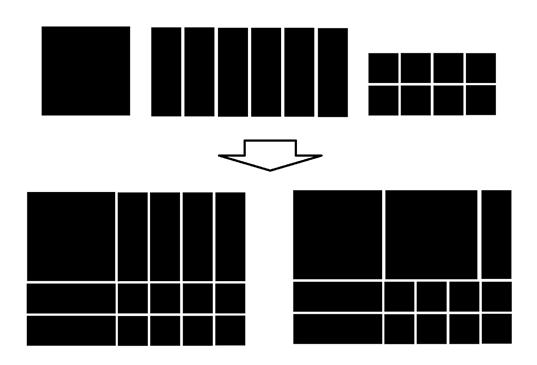Ｘ２＋６Ｘ＋８

係数が負の場合

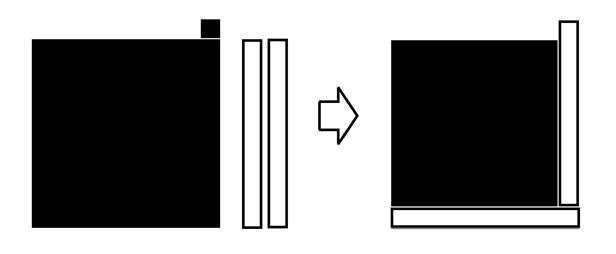Ｘ２－２Ｘ＋１　 → 　（Ｘ－１）（Ｘ－１）

では、Ｘ２＋２Ｘ－３の問題はどうでしよう。上の問題と同様に考えるのであれば、－３は１のタイルを３枚引くと考えればよいことになります。しかし、これではいっこうに解決がつきません

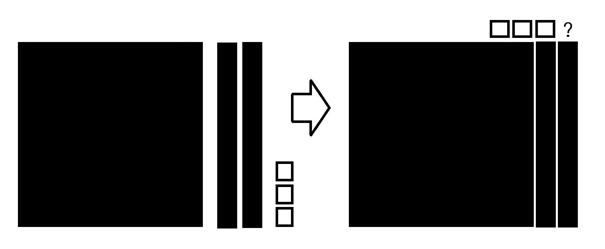　　Ｘ２＋２Ｘ－３　　　　長方形にならない

このような場合は、このタイル因数分解を負の整数まで可能にするためのちょっとしたアイデアが必要になります。そのアイデアというのが「隠れ板」の考え方です。

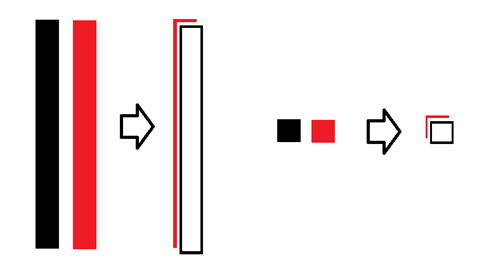Ｘと－Ｘで０になる。　１と－１で０になる

そうすると、Ｘ２＋２Ｘ－３はＸ２＋２Ｘ－３
　　　　　　　　　　　　　　　　　↓ 　　
Ｘ２＋３Ｘ－Ｘ－３　 → 　（Ｘ－１）（Ｘ＋３）

Ｘ２＋ｐＸ＋ｑのパターン分け

式のパターンは、ｐ，ｑが正か負かによって次の４つの場合が考えられます。操作の仕方などの特徴を整理できるとよいでしょう。

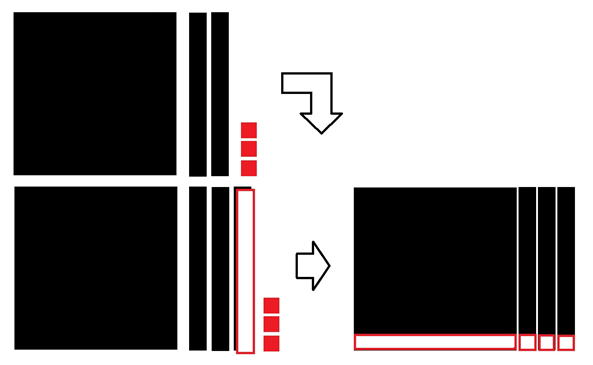
① ｐ＞０，ｑ＞０の場合

Ｘ２＋４Ｘ＋３　→ （Ｘ＋１）（Ｘ＋３）

② ｐ＜０，ｑ＞０の場合

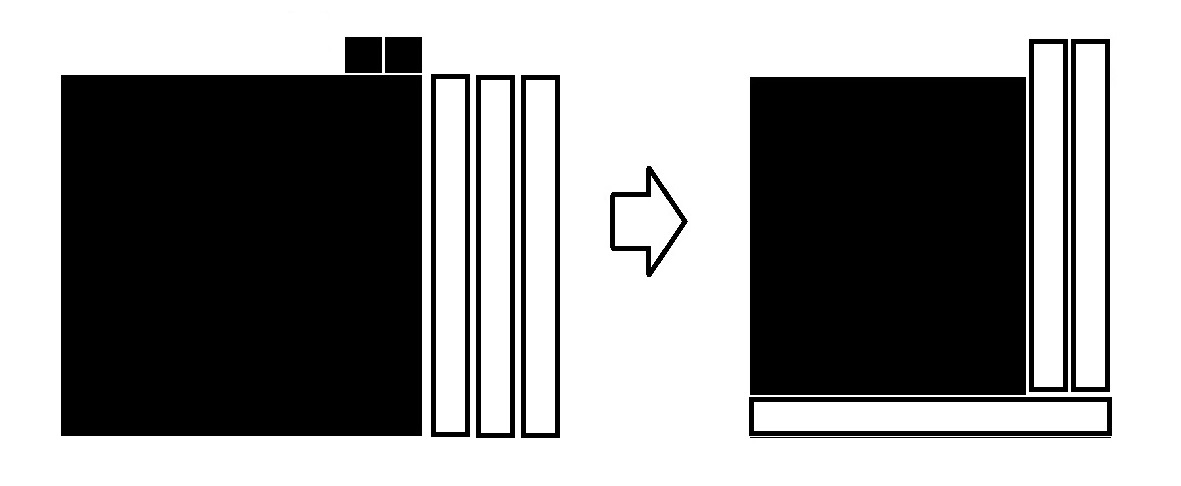Ｘ２－３Ｘ＋２　 → 　（Ｘ－１）（Ｘ－２）

ある量を加え、次に同じ量だけ取り去るならば最初と同じ量である。

③ ｐ＞０，ｑ＜０の場合

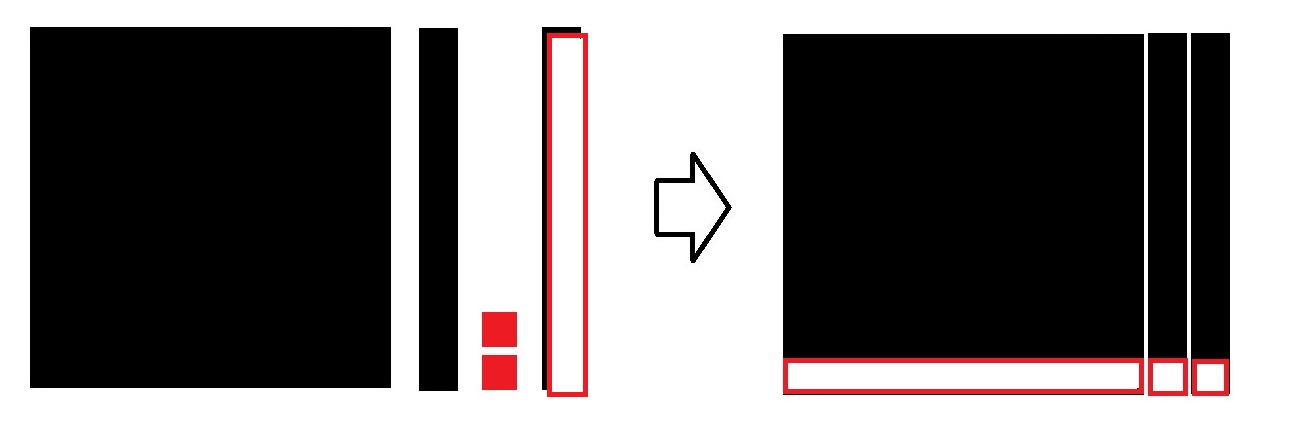Ｘ２＋Ｘ－２（Ｘ２＋２Ｘ－Ｘ―２）
→ （Ｘ－１）（Ｘ＋２）

④ ｐ＞０，ｑ＞０の場合

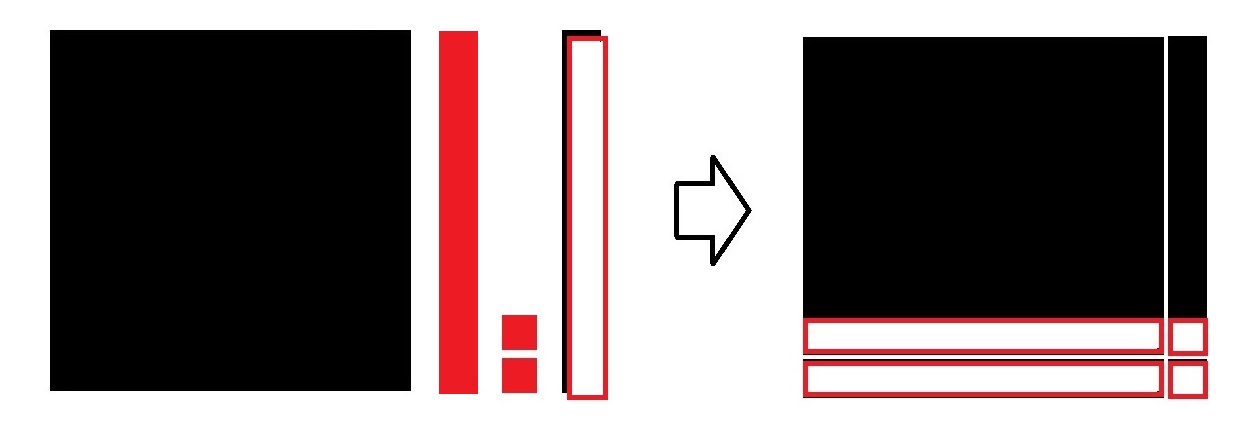Ｘ２－Ｘ－２（Ｘ２－２Ｘ＋Ｘ－２）
→ 　Ｘ＋１）（Ｘ－２）

Ｘ２＋ｐＸ＋ｑ＝（Ｘ＋ａ）（Ｘ＋ｂ）において、ｐ，ｑ，ａ，ｂは整数です。このとき、どんなｐ，ｑに対してもａ，ｂが存在するとは限りません。このことをいろいろな問題を作って確認してみましょう。

二次方程式を解く

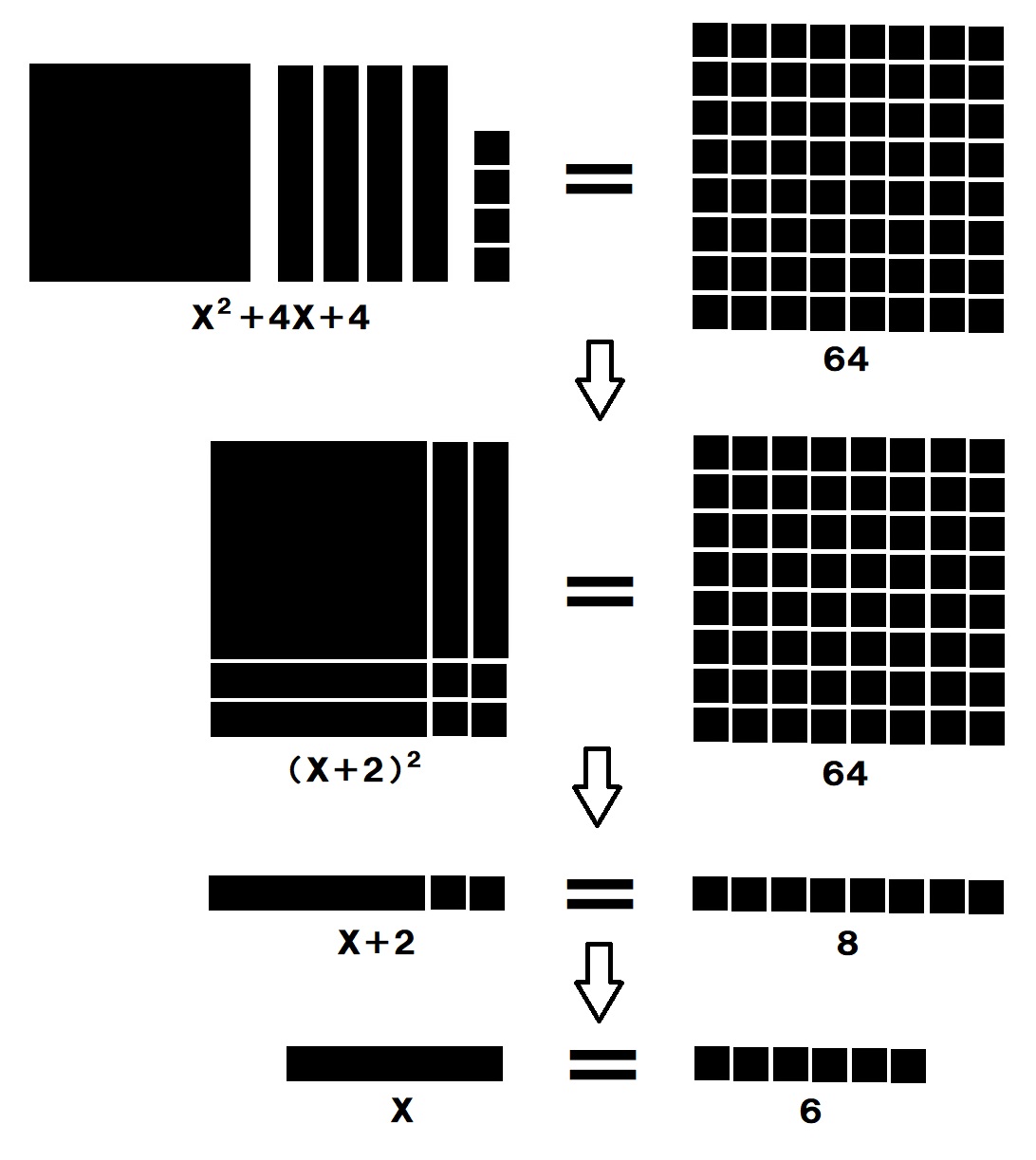
タイル因数分解の考え方が理解できたならば、二次方程式の解を求めることもできます。（当然自然数の範囲ですが）たとえば、Ｘ２＋４Ｘ＋４＝６４ならば

この正方形での形がすめば、長方形も同様に考えて解を求めることができそうですが、Ｘの値が負になる場合は新たなアイデアがないと解決できません。したがって、因数分解学習でとどめておく方がよいでしょう。

Ｘ２＋３Ｘ＋２＝０ → （Ｘ＋１）（Ｘ＋２）＝０　　　　　　　　
→ （Ｘ＋３）＝０又は（Ｘ＋２）＝０

おわりに

正方形のタイルの代わりに正三角形や平行四辺形のタイルでも同じように説明できるのではないだろうか。正方形のタイルの代わりに立方体を使ったら３次式の因数分解ができるのではないだろうか。いろいろ発展的に考えていけるとおもしろい。